MÉTODO DE GAUSS-SEIDEL
Idéia principal:
Cada coordenada do vetor correspondente à nova aproximação é calculada a
partir da respectiva equação do sistema, utilizando-se as coordenadas do
vetor aproximação da iteração anterior, quando essas ainda não foram
calculadas na iteração corrente, e as coordenadas do vetor aproximação da
iteração corrente, no caso contrário.
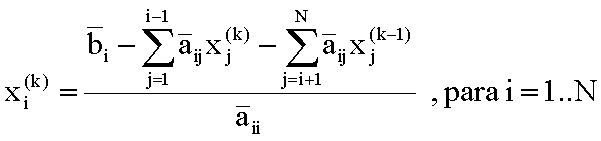
EXEMPLO ILUSTRATIVO:

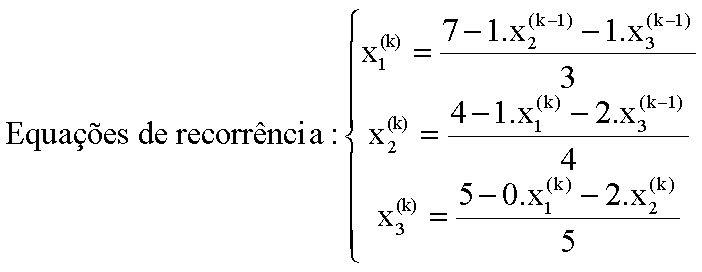
|
Iteração |
{x}(k) |
|
1 |
2.3333 0.4167 0.8333 |
|
2 |
1.9167 0.1042 0.9583 |
|
3 |
1.9792 0.0260 0.9896 |
|
4 |
1.9948 0.0065 0.9974 |
|
5 |
1.9987 0.0016 0.9993 |
|
6 |
1.9997 0.0004 0.9998 |
|
7 |
1.9999 0.0001 1.0000 |
|
... |
... |
|
Solução
exata |
2.0000 0.0000 1.0000 |