Zeros de Funções
Métodos Numéricos - A partir de um intervalo

• Pré-requisitos:

  • Considere uma função f(X) contínua dentro de um intervalo [a, b];

  • Considere ainda que nos extremos do intervalo [a, b] a função estudada apresente sinais contrários, ou seja, f(a)*f(b)<0.

• Resultado:

  • Garante-se a existência de pelo menos um zero dessa função dentro do intervalo [a, b].

• Idéia:

  • Encontrar um intervalo menor que o intervalo original e que atenda aos pré-requisitos acima mencionados;

  • Repetir o procedimento anterior até que se atinja o critério de tolerância de determinação do zero da função.

• Estratégia de diminuição do intervalo:

  • Nenhum cuidado especial é necessário para garantir o primeiro pré-requisito uma vez que toda função contínua em um intervalo, também será contínua em qualquer subintervalo menor;

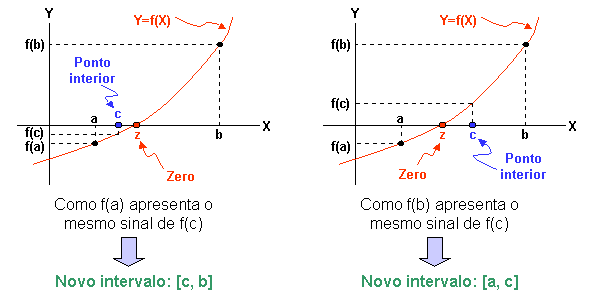
  • Para garantir que nesse novo intervalo a função continue a apresentar sinais contrários, deve-se:

    • Escolher um ponto c dentro do intervalo original [a, b];

    • Redefinir o novo intervalo substituindo o extremo cujo sinal da função é o mesmo que no ponto escolhido.

[Volta]