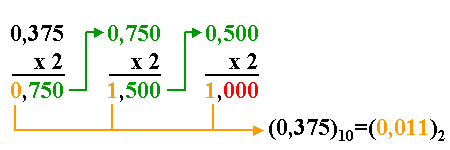SISTEMAS DE REPRESENTAÇÃO NUMÉRICA

Números inteiros:

• (d_Nd_N-1...d₂d₁d₀)_b onde d_i é um dígito da base b em questão.

• Cada dígito apresenta b possibilidades: 0, 1, 2 ... b-1.

• Exemplos:

  • (3928)₁₀=8x10⁰+2x10¹+9x10²+3x10³ ... base decimal;

  • (11001)₂=1x2⁰+0x2¹+0x2²+1x2³+1x2⁴ ... base binária.

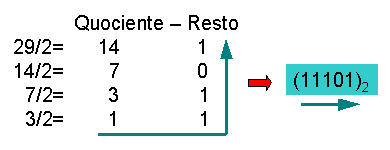
• Conversão da base entre as bases decimal e binária:  

  • B>D: (11001)₂=1x2⁰+0x2¹+0x2²+1x2³+1x2⁴=1+0+0+8+16=(25)₁₀

  • D>B: (29)₁₀=(?)₂

  
  
  

• O sistema de representação binário é compatível com a unidade básica de informação do computador (bit - circuito onde passa ou não corrente).

• Por limitação física, reserva-se uma quantidade finita de bits para o armazenamento do número inteiro, estabelecendo-se um intervalo finito para esses números. No caso de ultrapassar os limites desse intervalo, ocorrerá um erro do tipo overflow.

• Um bit é exclusivo para representação do sinal do número inteiro.

Números reais:

• (d_Nd_N-1...d₂d₁d₀,d_-1d_-2d_-3...d_-M+1d_-M)_b onde d_i é um dígito da base b em questão.

• Assim como para os números inteiros, cada dígito apresenta b possibilidades: 0, 1, 2 ... b-1.

• Exemplos:

  • (39,28)₁₀=(9x10⁰+3x10¹)+(2x10^-1+8x10^-2) ... base decimal;

  • (110,01)₂=(0x2⁰+1x2¹+1x2²)+(0x2^-1+1x2^-2) ... base binária.

• Conversão da base entre as bases decimal e binária:  

  • B>D: (110,01)₂=(0x2⁰+1x2¹+1x2²)+(0x2^-1+1x2^-2)=(0+2+4)+(0,0+0,25)=(6,25)₁₀

  • D>B: (14,375)₁₀=(?)₂

    • Converte-se a partir inteira do número igualmente ao que foi proposto anteriormente, ou seja, (14)₁₀=(1110)₂

    • Converte-se a parte fracionária através de multiplicações sucessivas pelo número dois, armazenando-se e eliminando-se o inteiro do resultado até que sua parte fracionária seja zero (Confira o exemplo a seguir).

    

     

    • Conclusão: (14,375)₁₀=(1110,011)₂

  • Atenção: Nem todo número real na base decimal possui uma representação finita na base binária. Experimente converter o número (0,1)₁₀. 

[Anterior]  [Volta]  [Próxima]